集成模型
Bagging
多个弱模型取均值
Boosting
多个弱模型累加,且后一模型是在前一模型的基础上生成的,是一种迭代思路。
stacking
几种方法的主要区别

随机森林
训练样本的随机化
- 有放回的
特征选择的随机化
- 简单随机采样
- 信息熵法
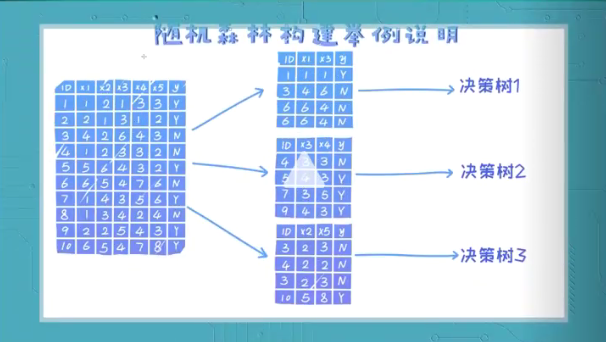
- Bagging包括随机森林,随机森林隶属于Bagging
- 鲁棒性如何解释?对极端数据(噪声,扰动)的处理能力,能一定程度上可以应对数据异常数据。
- 为什么要集成学习?一个单一模型很容易过拟合
GBDT(Boosting)
- bagging用来解决过拟合,有可能会欠拟合。boosting解决欠拟合,有可能会过拟合。
- 将前一阶段的残差作为下一阶段的因变量
- 累加求最终预测值
XGBoost(Boosting)
- 目标函数可以用泰勒展开
- 与原本boosting的区别,XGboost加入了正则化,传统boosting只用了一阶导,XGboost作了泰勒展开,有二阶导
Boost中目标函数不一定是多项式,直接求导比较难。
- XGboost
以泰勒展开将非多项式目标函数转化为多项式。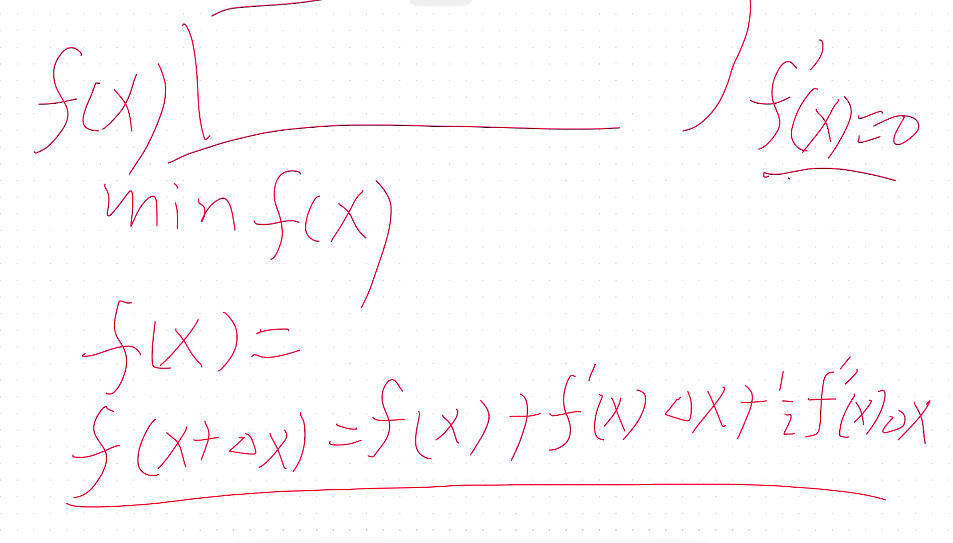
叠加式训练
- 递推的内容

- 二元交叉商

- 目标函数的解释
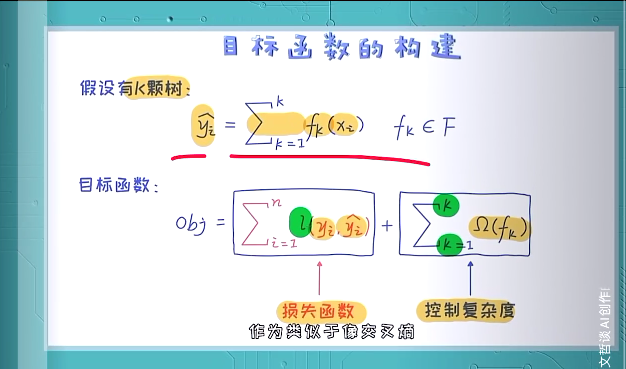
垃圾邮件分类(典型分类问题)
贝叶斯


似然(词频统计)
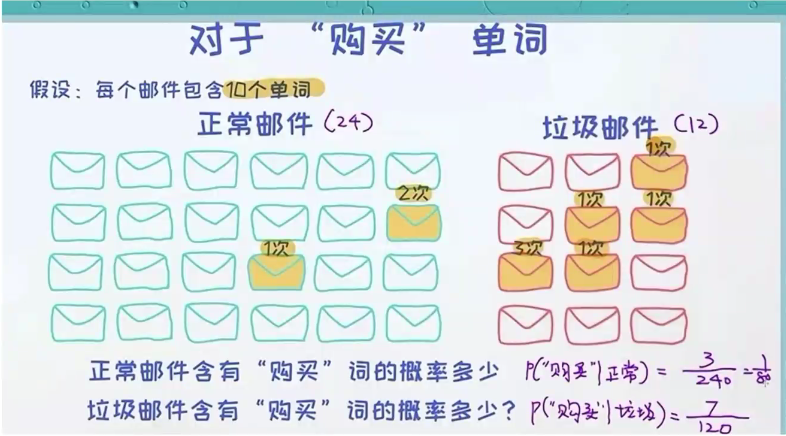
先验概率

目的(做出判断)
通过条件概率来进行比较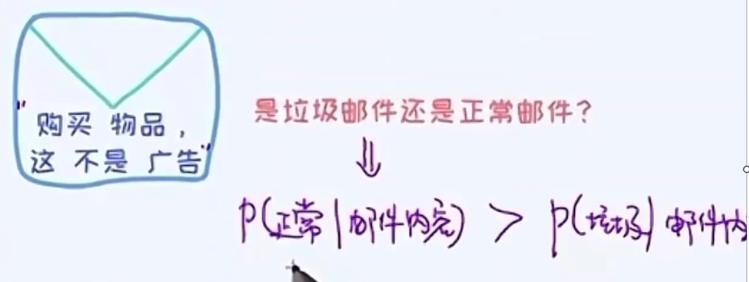
分母为固定常数,便于比较
- 避免概率为0的情况——加1平滑

最大问题:
- 不能保证特征间的独立性,未考虑到特征间的相关性,只是根据样本出现的次数,进行基于概率的训练。只是强调某个x是某个y的条件。
- 只能用原始特征,不能加工或提取新特征。
- 为什么要+1平滑,防止出现概率为0的情况。
优点:
贝叶斯不容易过拟合——异常值、缺失值概率极低,基本可以视为被舍弃了,所以受异常值影响比较低。
层次聚类
树形图
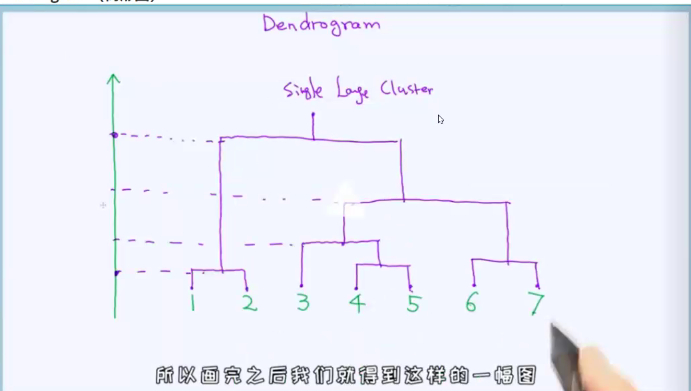
凝聚聚类(自下而上)
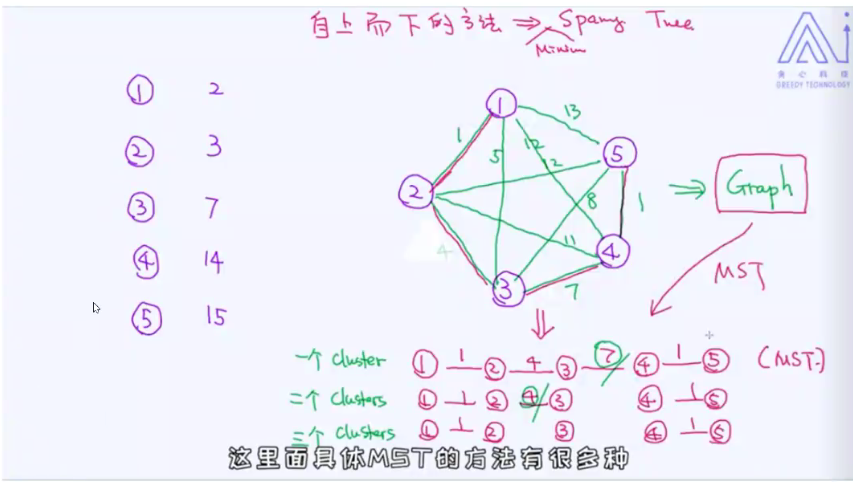
分裂聚类(自上而下)
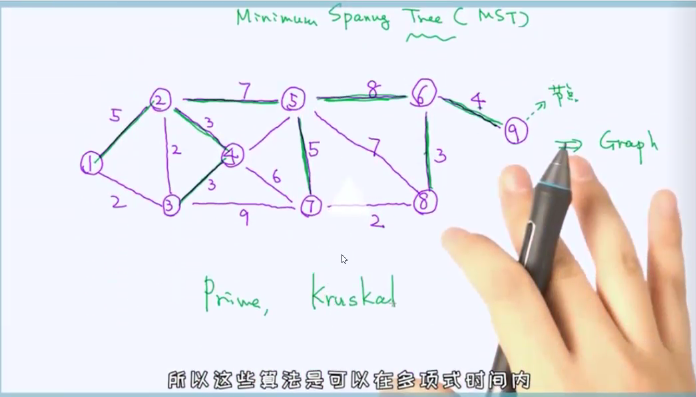
MST(最小生成树)