特征选择
为什么要进行特征选择?
特征过多导致过拟合、有一些特征是噪音。
特征选择技术:
1、 尝试所有组合:也是全局最优
2、贪心算法:每次决策都是基于当前情况去寻找最优解。计算过程:把特征加进去→是否更优?→是:加入模型/否:淘汰
3、L1正则:目标函数为损失函数;特点:具有稀疏性
4、决策树:节点代表每个特征选择。优点:便于处理高维数据
5、相关性计算:一种脱离模型内部结构而直接分析特征$x_i$和标签y的相关性的方法。主要是计算向量相似度的方法。
总结:都是对比了各个特征的优劣,如何计算优劣的方法不同。
L1正则化
次梯度下降
L1正则特征选择问题
弹性网络回归
1、计算上:
(1)相关性:计算$x_i、y_i$,扔掉差的
(2)主成分:只计算$x_i$
问题:
(1) 为什么信息熵这么计算?
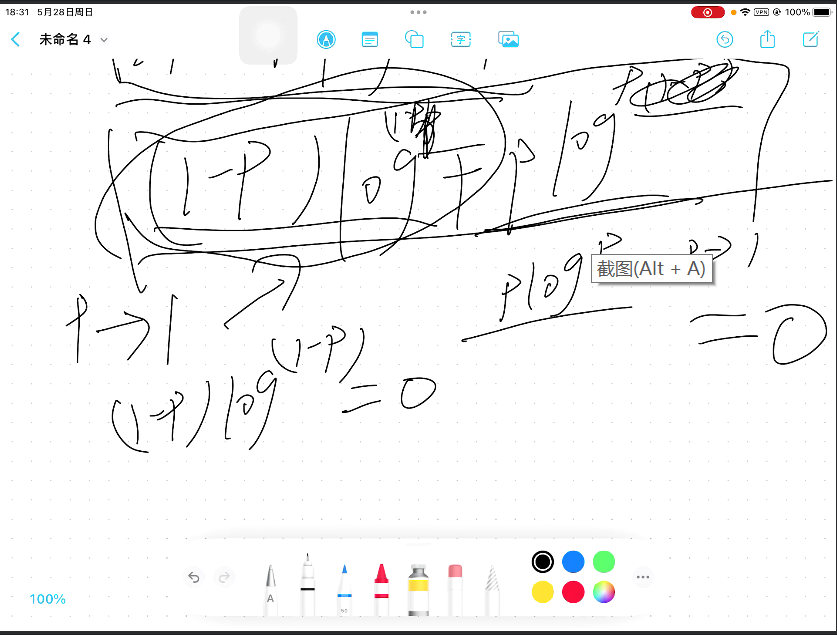
信息熵在神经网络里面也叫交叉熵,所有二分类问题都是这么算的。交叉熵在预测对的时候p为0/1,如果是0.5那么是不对的。
(2) 贪心算法为什么降低了复杂度?
假设使用贪心算法,有ABCDE五个选项,并两两组合。第一次先选D做组合,即DA、DB、DC、DE,下一次再选C做组合,这时候只用考虑CA、CB、CE,不用考虑CD,以此类推。
(3) L1正则化有什么缺点?
有一些点被扔掉了,而且是随机扔掉的。我们希望挑一个全局最好的扔掉,但是它是挑一个局部最好的扔掉。
决策树
决策树的定义
决策树的分类:
1、分类决策树 / 回归决策树
2、二叉树 / 多叉树
决策树算法:
CART算法只能构建二叉树,其他算法可以构建多叉树
有些只可以做回归或者分类
一颗决策树对应的决策边界:
需要学习:1.树的形状 2. 每一个决策的阈值$\theta_1$ 3. 叶节点的值
好的特征特点:
分类后不确定性变小
不确定性——信息熵
事情发生的概率很低:信息熵很高
事情发生的概率很高:信息熵很低
log取2信息量是比特,取1是奈特
决策树:原来的不确定性(划分前的)-分割后的不确定性(划分后的)=不确定性的减小(信息熵-条件熵=信息增益)
信息增益最大的作为根节点:$f_2>f_1$,所以$f_2$作为根节点
问题:
(1)决策树的根节点和叶节点代表什么?
根节点:输入方向;叶节点:判别指标,就是分为哪一类。也就是说,根节点是指标,最后那个叶节点是标签。根节点是输入,叶节点是输出。
(2)决策树的作用
决策树的作用:分类和回归。注意:三种树只有CART才能做回归。
(3)决策树的决策边界和线性回归的边界有什么区别?
之前线性回归边界都是二分类,现在决策边界可以包含多分类,可以有多个区域。
(4)信息熵为什么取对数?
避免他们之间的差距过大,比如一个概率是log0.01,另一个是log0.09。
上面0.01次方和0.02次方差距会很明显,混乱程度会加剧,从而更容易做决策。
数据处理取对数:核心是为了差距变得更大(0-1之间)或更小(1以上)
(5)信息熵是做什么的?
信息熵就是在算平均信息量。
构建决策树
问题:
(1)特征一样、标签不一样的数据要不要删除?
这种数据不能删,因为这种数据会提供一定的不确定性,如果删掉信息熵会一下子降低,会导致结果变得很差。
(2)决策树中唯一路径是什么?
给一条路径,可以一条路走到底的。
(3)什么是深度?
做几次判断,深度就有多少。最大的判断值为树的深度。
(4)什么时候不用继续分类?
一条路走到底,都是F或者都是N,就可以不用继续分类。
(5)同一个样本,结果既是F也是N,这是什么情况?
同个标签但又F和N,这条样本是在决策边界上,这类数据的作用是告诉你什么地方是决策边界。这类样本是不能删除的。
决策树性能
决策树性能:提升性能——防止过拟合,越简单越好
如何避免决策树的过拟合?
最大深度对模型准确率的影响
问题:
(1)决策树过拟合有哪些原因?
数据不行:有用的特征都没有,如学习成绩和他平时吃什么。
特征样本里出现噪声
某个地方信息熵有错误,随着迭代错误越来越放大
解决方法:
剪枝(修改一些叶节点)
设置最大深度
集成学习
(2)多重比较是什么?
每次进行比较的时候都会出现错误,树的深度一旦大了,会涉及到一个过多的比较过程,错误会越来越多,误差也会随之累加起来,变得越来越大。
回归树如何构建
回归问题中量化不确定性:标准差(分类是信息熵)
问题:
(1)回归树和分类树的区别?
计算方法:回归树选择根节点是用标准差来选,分类树是信息熵去选。条件熵是差不多的
(2)回归树中如何确定标签?
决策树分裂完是同一个标签,是或者否。而回归树是有一个阈值的,就是标准差小于某个数字,那么分类就结束了。